Latent Growth Curve Modeling
Latent Growth Curve Modeling (LGCM) is a powerful statistical technique that has revolutionized the way researchers analyze longitudinal data, especially in the fields of psychology, education, and social sciences. With its ability to capture and understand complex patterns of change over time, LGCM has become an invaluable tool for researchers seeking to uncover hidden trends and make accurate predictions.
In this comprehensive guide, we will delve deep into the world of Latent Growth Curve Modeling, exploring its theoretical foundations, practical applications, and the immense potential it holds for shaping our understanding of dynamic systems. Through real-world examples and step-by-step demonstrations, we aim to provide an expert-level overview of this cutting-edge statistical approach, empowering researchers and practitioners to harness its full potential.
Unraveling the Dynamics of Change: An Introduction to Latent Growth Curve Modeling
At its core, Latent Growth Curve Modeling is a technique used to analyze and interpret longitudinal data, focusing on the underlying growth patterns and trajectories. Unlike traditional statistical methods that treat data points as independent, LGCM acknowledges the interconnectedness of data collected over time, allowing for a more nuanced understanding of change processes.
The beauty of LGCM lies in its ability to capture both the when and the how of change. By modeling the latent growth curve, researchers can estimate individual growth trajectories, identify different growth patterns, and explore the factors influencing these changes. This approach not only provides a more comprehensive view of the data but also enables the prediction of future outcomes based on observed patterns.
Imagine a study tracking the academic performance of students over several years. With LGCM, researchers can go beyond simple averages and standard deviations to understand how individual students' grades change over time, identify those at risk of falling behind, and potentially intervene to support their academic growth.
Theoretical Foundations: Building Blocks of Latent Growth Curve Modeling
To grasp the full potential of LGCM, it is essential to understand its theoretical underpinnings. LGCM is rooted in structural equation modeling (SEM), a powerful statistical framework that allows for the estimation of complex relationships between observed and latent variables.
At its simplest, LGCM can be seen as an extension of linear regression, where the dependent variable is not a single outcome but a series of outcomes measured repeatedly over time. However, LGCM goes beyond this by incorporating latent variables to represent the underlying growth processes.
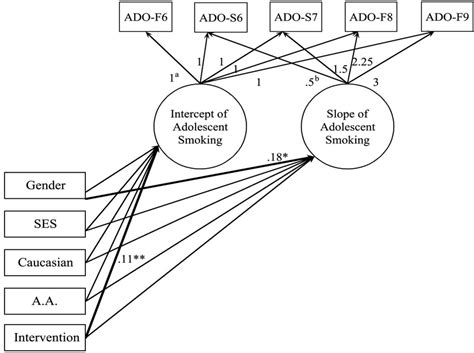
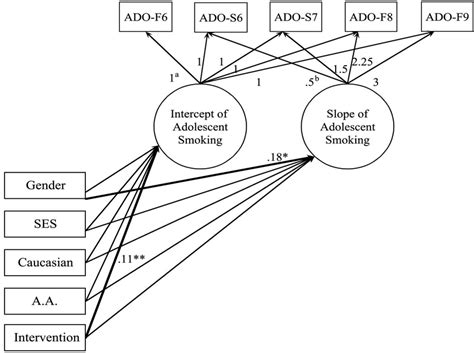
The key components of LGCM include:
- Latent Growth Factors: These represent the unobserved, underlying dimensions of change. For example, in a study on physical development, latent growth factors might represent height and weight trajectories.
- Growth Curve Parameters: These parameters define the shape of the growth curve, including the initial status, the rate of change, and potentially other higher-order effects like quadratic or cubic trends.
- Measurement Model: This component specifies the relationship between the observed data (e.g., test scores, behavior ratings) and the latent growth factors. It helps to estimate the reliability and validity of the measurements.
- Structural Model: The structural model explores the relationships between the growth curve parameters and other variables of interest, such as demographic factors or treatment conditions.
By combining these components, LGCM allows researchers to estimate complex growth trajectories, investigate individual differences in growth patterns, and explore the factors that influence these changes.
Practical Applications: Unlocking the Power of LGCM
The versatility of Latent Growth Curve Modeling is evident in its wide range of applications across various fields. Here, we explore some real-world examples to illustrate the practical impact of LGCM.
Educational Research: Tracking Student Progress
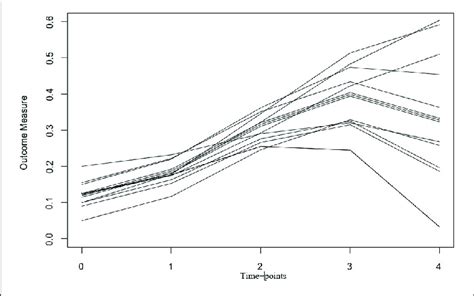
In educational settings, LGCM has proven invaluable for tracking student progress over time. By modeling the growth trajectories of academic performance, researchers can identify high-achieving students, those at risk of falling behind, and the factors influencing their growth.
For instance, a study using LGCM might examine the reading comprehension skills of elementary school students across multiple grades. By analyzing the growth curves, researchers can identify students with rapid growth, steady progress, or those experiencing stagnation. This information can guide educational interventions, ensuring that students receive the support they need to thrive.
| Student Group | Growth Trajectory |
|---|---|
| High Achievers | Steady increase in reading comprehension |
| Struggling Readers | Stagnation or slight decline |
| Rapid Improvers | Steep increase in skills over time |
Psychological Studies: Understanding Personal Growth
LGCM finds extensive application in psychological research, particularly in studies exploring personal development and change. By modeling growth curves, researchers can gain insights into the trajectories of various psychological constructs, such as self-esteem, resilience, or cognitive abilities.
Consider a longitudinal study on self-esteem development in adolescents. LGCM can help identify different patterns of self-esteem growth, such as consistent high self-esteem, gradual improvement, or a decline followed by recovery. This understanding can inform interventions aimed at promoting positive self-esteem and mental well-being.
Social Sciences: Analyzing Social Trends
In the realm of social sciences, LGCM offers a powerful tool for analyzing social trends and dynamics. From understanding the evolution of attitudes and beliefs over time to tracking the spread of social movements, LGCM provides a comprehensive framework for capturing and interpreting complex social phenomena.
For example, a study on the adoption of new technologies might use LGCM to model the growth curve of technology usage among different demographic groups. This analysis can provide insights into the factors influencing technology adoption, helping policymakers and businesses make informed decisions.
Advanced Techniques: Expanding the Horizons of LGCM
While the basic principles of Latent Growth Curve Modeling are powerful in their own right, researchers have developed a range of advanced techniques to enhance its capabilities and address specific research questions.
Multigroup Latent Growth Curve Modeling
Multigroup LGCM allows researchers to compare growth trajectories across different groups, such as demographic categories, treatment conditions, or cultural contexts. This technique provides insights into whether the growth patterns differ between groups and the factors contributing to these differences.
For instance, a study on the effectiveness of a new teaching method might use multigroup LGCM to compare the growth trajectories of students in experimental and control groups. By analyzing the differences in growth curves, researchers can assess the impact of the teaching method and identify any potential disparities in learning outcomes.
Latent Class Growth Analysis
Latent Class Growth Analysis (LCGA) is a variation of LGCM that focuses on identifying distinct growth trajectories or classes within a population. This technique is particularly useful when researchers suspect that there may be unobserved subgroups with different growth patterns.
Imagine a study on weight loss programs. LCGA can help identify different classes of participants based on their weight loss trajectories, such as rapid responders, steady losers, and plateauers. This information can guide the development of tailored interventions for each subgroup.
Longitudinal Mediation Analysis
Longitudinal Mediation Analysis extends LGCM by exploring the mediating effects of latent variables on the relationship between two observed variables measured over time. This technique is valuable for understanding the underlying mechanisms driving change processes.
For example, in a study on the impact of physical activity on cognitive function in older adults, longitudinal mediation analysis can be used to examine whether the relationship between physical activity and cognitive performance is mediated by changes in brain structure or function.
Challenges and Considerations: Navigating the Complexities of LGCM
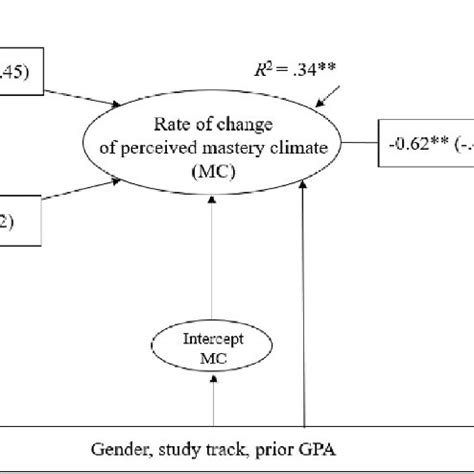
While Latent Growth Curve Modeling offers immense potential, it also presents several challenges and considerations that researchers must address to ensure the validity and reliability of their analyses.
Sample Size and Power Considerations
LGCM, being a complex statistical technique, requires relatively large sample sizes to ensure sufficient statistical power. Researchers must carefully plan their studies to ensure an adequate number of participants, especially when dealing with multiple groups or complex models.
Model Specification and Identification
The choice of model specification is a critical aspect of LGCM. Researchers must carefully consider the number and type of latent growth factors, the functional form of the growth curve (linear, quadratic, etc.), and the inclusion of higher-order effects. Inappropriate model specification can lead to biased estimates and erroneous conclusions.
Missing Data and Imputation
Longitudinal studies often face the challenge of missing data, especially when participants drop out over time. LGCM has specific methods for handling missing data, but researchers must carefully consider the patterns of missingness and choose appropriate imputation techniques to minimize bias.
Interpretation of Results
Interpreting the results of LGCM analyses requires a deep understanding of the theoretical framework and the specific research question being addressed. Researchers must be cautious when interpreting growth curve parameters, ensuring that their conclusions are supported by the data and the underlying assumptions of the model.
Future Directions: Expanding the Horizons of Latent Growth Curve Modeling
The field of Latent Growth Curve Modeling is continuously evolving, with researchers exploring new avenues and pushing the boundaries of what is possible. Here, we highlight some of the emerging trends and future directions that hold promise for further enhancing the capabilities of LGCM.
Integration with Machine Learning
The integration of LGCM with machine learning techniques offers exciting possibilities for automating model selection, optimizing parameter estimation, and improving the prediction of future outcomes. By combining the strengths of both fields, researchers can develop more efficient and accurate modeling approaches.
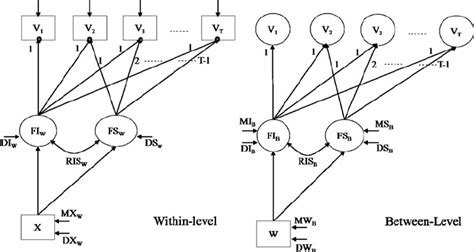
Multilevel Latent Growth Curve Modeling
Multilevel LGCM extends the traditional approach by incorporating hierarchical structures, such as students nested within classrooms or patients within healthcare facilities. This technique allows for the exploration of growth processes at multiple levels, providing a more nuanced understanding of complex systems.
Dynamic Systems Modeling
Dynamic Systems Modeling (DSM) takes LGCM a step further by incorporating feedback loops and complex interactions between variables. DSM allows for the simulation of dynamic systems, providing a powerful tool for predicting the long-term consequences of interventions or policy changes.
Longitudinal Meta-Analysis
Longitudinal Meta-Analysis applies LGCM techniques to synthesize and analyze results from multiple longitudinal studies. By pooling data across studies, researchers can gain insights into the generalizability of growth trajectories and identify consistent patterns across different populations or contexts.
Conclusion: Empowering Research with Latent Growth Curve Modeling
Latent Growth Curve Modeling has emerged as a powerful tool for researchers seeking to understand the dynamics of change and development. By capturing the complexities of longitudinal data, LGCM offers a comprehensive framework for analyzing growth trajectories, identifying individual differences, and predicting future outcomes.
From educational research to psychological studies and social sciences, the applications of LGCM are vast and impactful. With its ability to provide nuanced insights and guide informed decision-making, LGCM is shaping the future of research across diverse fields. As the field continues to evolve, we can expect even more sophisticated techniques and applications, further enhancing our understanding of dynamic systems.
How does LGCM compare to traditional longitudinal analysis methods?
+
LGCM offers several advantages over traditional methods. It provides a more nuanced understanding of growth processes by modeling individual trajectories and capturing complex patterns of change. LGCM also allows for the estimation of growth curve parameters, which can be used to predict future outcomes and make informed decisions.
What software can be used for LGCM analysis?
+
Several software packages are available for LGCM analysis, including Mplus, R (with packages like lavaan), and Stata. These programs offer user-friendly interfaces and powerful tools for model estimation and interpretation.
Are there any limitations to LGCM’s applicability?
+
While LGCM is a powerful technique, it does have some limitations. It requires relatively large sample sizes and well-designed longitudinal studies to ensure accurate results. Additionally, the complexity of LGCM models can make interpretation challenging, requiring a deep understanding of the theoretical framework.



